(20分)一半径R=0.6m的金属圆筒有一圈细窄缝,形状如图所示。圆筒右侧与一个垂直纸面向里的有界匀强磁场相切于P,圆筒接地,圆心O处接正极,正极与圆筒之间的电场类似于正点电荷的电场,正极与圆筒之间电势差U可调。正极附近放有一粒子源(粒子源与正极O间距离忽略不计)能沿纸面向四周释放比荷q/m=1.5×l05C/kg的带正电粒子(粒子的初速度、重力均不计)。带电粒子经电场加速后从缝中射出进入磁场,已知磁场宽度d=0.4m,磁感应强度B=0.25T。
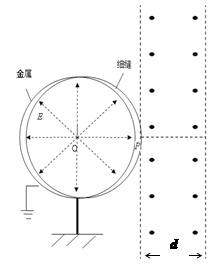
(1)若U=750V,求:①粒子达到细缝处的速度;②若有一粒子在磁场中运动的时间最短,求此粒子飞出磁场时与右边界的夹角大小。
(2)只要电势差U在合适的范围内变化,总有从向沿某一方向射出粒子经过磁场后又回到O处,求电势差U合适的范围。
(1)①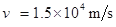 ②600;(2)
②600;(2)
题目分析:(1)①若U=750V,粒子经电场得
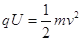 (2分)
(2分)
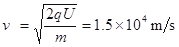 (1分)
(1分)
②粒子在磁场中做匀速圆周运动得  (2分)
(2分)
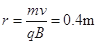 (1分)
(1分)

粒子在磁场中运动轨迹对应的弦长L=d=0.4m时运动的时间最短,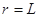 (2分)
(2分)
则粒子飞出磁场时与右边界的夹角大小  (2分)
(2分)

(2)粒子射入磁场后与右边界相切时,正极与圆筒之间电势差最大为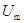 ,由几何关系得
,由几何关系得
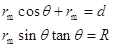 (2分)
(2分)
得  ,
,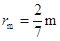 (1分)
(1分)
粒子在磁场中 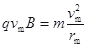 (2分)
(2分)
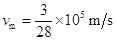 (1分)
(1分)
粒子经电场中 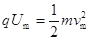 (2分)
(2分)
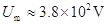 (1分)
(1分)
电势差U合适的范围: (1分)
(1分)
