问题
计算题
如图甲所示，质量分别为m1＝1kg和m2＝2kg的A、B两物块并排放在光滑水平面上，若对A、B分别施加大小随时间变化的水平外力F1和F2，其中F1＝（9-2t）N，F2＝（3＋2t）N，请回答下列问题：
（1）A、B两物块在未分离前的加速度是多大？
（2）经多长时间两物块开始分离？
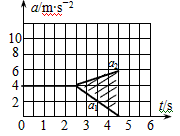
（3）在图乙的坐标系中画出两物块的加速度a1和a2随时间变化的图像。
（4）速度的定义为v＝Δx/Δt，“v-t”图像下的“面积”在数值上等于位移Δx；加速度的定义为a＝Δv/Δt，则“a-t”图像下的“面积”在数值上应等于什么?
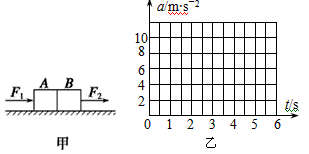
答案
解析：（1）对A、B整体，由牛顿第二定律： F1+F2＝(m1+m2)a①
故a=
= 4m/s2②
（2）当A、B间的弹力为0时，A、B分离，分离时： 
=
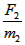③
即
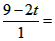
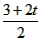④
可求出t=2.5s⑤
（3）由（1）问知，A、B分离之前（2.5s之前），A、B加速度相同；
分离后，对A：a1=
=
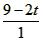m/s2=（
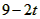）m/s2，图像如图所示
对B：a2=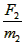
=
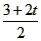m/s2=（1.5 + t）m/s2，图像如图所示
（4）面积是速度的变化量Δv。