问题
计算题
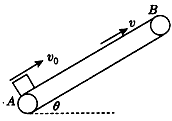
如图所示，为皮带传输装置示意图的一部分，传送带与水平地面的倾角θ=370，A、B两端相距5.0m，质量为M=10kg的物体以v0=6.0m/s的速度沿AB 方向从A端滑上传送带，物体与传送带间的动摩擦因数处处相同，均为0.5。传送带顺时针运转的速度v= 4.0m/s，（g取10m/s2，sin370=0. 6，cos370=0.8）求：
（1）物体从A点到达B点所需的时间；
（2）若传送带顺时针运转的速度可以调节，物体从A点到达B点的最短时间是多少？
答案
解：（1）设在AB上运动的加速度大小为a，由牛顿第二定律得mgsinθ十μmgcosθ=ma1①
设经t1速度与传送带速度相同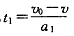
②
通过的位移
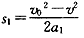③
速度小于v1至减为零前的加速度为mgsinθ-μmgcosθ=ma2④
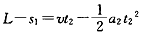⑤
物体继续减速，设经t2速度到达传送带B点，t=t1+t2=2.2s⑥
（2）若AB部分传送带的速度较大，沿AB上滑时所受摩擦力一直沿皮带向上，则所用时间最短，
此种情况加速度一直为a2，⑦
t=ls⑨。