如图所示是一个示波管工作原理图,电子经电压U1=4.5×103V加速后以速度V0垂直等间距的进入电压U2=180V,间距为d=1.0cm,板长l=5cm的平行金属板组成的偏转电场,离开电场后打在距离偏转电场s=10cm的屏幕上的P点,(e=1.6×10-19C,m=9.0×10-31kg)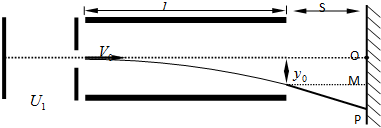
求:
(1)电子进入偏转电场时的速度V0=?
(2)射出偏转电场时速度的偏角tanθ=?
(3)打在屏幕上的侧移位移OP=?
(1)设电子经加速电场U1加速后以速度v0进入偏转电场,由动能定理有
qU1=
mv02,1 2
则有:v0=
=2qU1 m
=4×107m/s;2×1.6×10-19×4.5×103 9×10-31
故电子进入偏转电场的速度v0=4×107m/s;
(2)进入偏转电场后在电场线方向有,a=qU2 md
经时间t1飞出电场有t1=
,l v0
电场方向的速度vy=at1=
=qU2l mdv0
=4×106m/s;1.6×10-19×180×0.05 9×10-31×0.01×4×107
设射出偏转电场时速度的偏角为θ,则tanθ=
=vy v0
=4×106 4×107 1 10
(3)飞出电场时偏转量为y1=
at12 1 2
由以上各式得y1=
=U2 L 2 4dU1
=0.25cm; 180×0.052 4×0.01×4.5×103
设电子从偏转场穿出时,沿y方向的速度为vy,穿出后到达屏S所经历的时间为t2,
在此时间内电子在y方向移动的距离为y2,有:vy=at1
t2=s v0
y2=vyt2
由以上各式得
y2=U2sl 2dU1
故电子到达屏S上时,它离O点的距离:y=y1+y2=
(l+s)=U2l 4dU1
×(0.05+0.1)cm=0.75cm;180×0.05 4×0.01×4.5×103
答:(1)电子进入偏转电场时的速度4×107m/s;
(2)射出偏转电场时速度的偏角tanθ=
;1 10
(3)打在屏幕上的侧移位移OP=0.75cm.
