问题
解答题
设x1、x2是方程x2-6x+a=0的两个根，以x1、x2为腰和底边的等腰三角形只可以画出一个.试求a的取值范围.
答案
0＜a≤8或a=9
题目分析：设x1，x2为方程两根，且x1≤x2，则x1=3-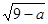
，x2=3+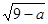，由x1＞0，x2＞0可得0＜a≤9，再分x1=x2、x1≠x2两种情况，结合等腰三角形的性质求解即可.
设x1，x2为方程两根，且x1≤x2，则x1=3-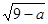，x2=3+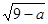
∵x1＞0，x2＞0
∴0＜a≤9
ⅰ当x1=x2时，即△=9-a=0，a=9时为正三角形
ⅱ当x1≠x2时，∵x1≤x2，∴以x2为腰为等腰三角形必有一个
而等腰三角形只有一个，故不存在以x2为底，x1为腰的三角形
∴2x1≤x2
∴6-2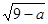≤3+
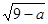
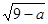∴≥1
∴0＜a≤8
综上所述：当0＜a≤8或a=9时只有一个等腰三角形.
点评：此类问题难度较大，综合性强，在中考中比较常见，需特别注意.