问题
解答题
求经过两直线l1:x-2y＋4=0和l2:x＋y-2=0的交点P，且与直线l3:3x-4y＋5=0垂直的直线l的方程.
答案
l的方程为y=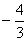
x＋2.
利用两条已知直线的方程组成方程组，其解为交点坐标，又直线l与3x-4y+5=0垂直，利用垂直直线的斜率之积为-1,可得直线l的斜率，然后按点斜式写出方程.
解方程组
可以得到P(0，2).
因为l3的斜率为
，所以直线l的斜率为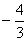，所以l的方程为y=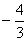x＋2.
