问题
解答题
△ABC中,D是BC边上任意一点(与B,C不重合),且|AB|2=|AD|2+|BD|·|DC|.求证:△ABC为等腰三角形.
答案
作AO⊥BC,垂足为O.
以BC所在直线为x轴,以OA所在直线为y轴,建立直角坐标系,如图3-3-2.
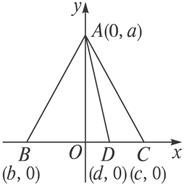
设A(0,a),B(b,0),C(c,0),D(d,0).
因为|AB|2=|AD|2+|BD|·|DC|,
所以,由距离公式可得b2+a2=d2+a2+(d-b)(c-d),
即-(d-b)(b+d)=(d-b)(c-d).
又d-b≠0,故-b-d=c-d,
即-b=c.
所以,△ABC为等腰三角形.
点到直线的距离公式

