问题
解答题
求过点(2,3)且在两轴上截距相等的直线方程.
答案
直线方程为y=-x+5或
.
由条件知该直线的斜率存在且不为0,由点斜式可设直线方程为y-3=k(x-2).
令x=0,得直线在y轴上截距为y=3-2k.
令y=0,得直线在x轴上截距为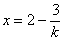
.
由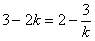
,得k=-1或
.
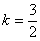故直线方程为y=-x+5或.
搜题请搜索小程序“爱下问搜题”
求过点(2,3)且在两轴上截距相等的直线方程.
直线方程为y=-x+5或.
由条件知该直线的斜率存在且不为0,由点斜式可设直线方程为y-3=k(x-2).
令x=0,得直线在y轴上截距为y=3-2k.
令y=0,得直线在x轴上截距为.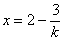
由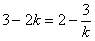,得k=-1或.
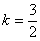故直线方程为y=-x+5或.