问题
解答题
已知点P(2,-1),求:
(1)过点P且与原点的距离为2的直线方程;
(2)过点P且与原点的距离最大的直线方程,并求出最大值.
(3)是否存在过点P且与原点的距离为6的直线?若存在,求出该直线的方程;若不存在,请说明理由.
答案
(1)适合题意的直线方程为x-2=0或3x-4y-10=0
(2)其方程为2x-y-5=0,且最大距离d=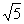 .
.
(3)不存在.
(1)当斜率不存在时,方程x=2适合题意.
当直线的斜率存在时,设为k,则直线方程应为y+1=k(x-2),即kx-y-2k-1=0.
根据题意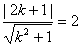 ,解得k=
,解得k=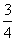 .
.
∴直线方程为 3x-4y-10=0.
∴适合题意的直线方程为x-2=0或3x-4y-10=0
(2)过点P且与原点的距离最大的直线方程应为过点P且与OP垂直的直线.易求其方程为2x-y-5=0,且最大距离d=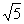 .
.
(3)不存在.由于原点到过点(2,-1)的直线的最大距离为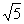 ,而6>
,而6>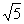 ,故不存在这样的直线.
,故不存在这样的直线.
