问题
计算题
为了安全，在公路上行驶的汽车之间应保持必要的车距。已知某地高速公路的最高限速v=110 km/h，假设前方车辆突然停止，后车司机从发现这一情况，经操纵刹车到汽车开始减速的时间t=0.50 s，刹车时汽车受到的阻力大小为车重的0.40倍，则该高速公路上汽车之间的安全车距至少为多少？（g取10 m/s2）
答案
解：高速公路的最高限速为v=110 km/h≈ 30.56m/s
由牛顿第二定律得，汽车刹车时的加速度为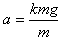
=kg=0.40×10 m/s2=4.0 m/s2
如果汽车以最高限速行驶，在司机的反应时间内，汽车做匀速直线运动，则运动的距离为x1=vt=30.56×0.50 m=15.28 m
汽车从最高限速开始刹车到停止所通过的距离为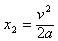
=
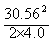m≈116.74 m
所以该高速公路上汽车间的距离至少为x=x1+x2=15.28 m+116.74 m=132.02 m