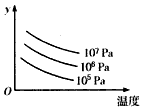
已知函数f(x)=2sinωx+cos(ωx+
(Ⅰ)求f(x)的最大值和最小值及相应的x的值; (Ⅱ)在△ABC中,若角A、B、C所对边分别为a、b、c,且f(B)=1,b=3
|
(Ⅰ)f(x)=2sinωx+cos(ωx+
)-sin(ωx-π 6
)-1=sinωx+π 3
cosωx-1=2sin(ωx+3
)-1--------------------(2分)π 3
由
=4π得ω=2π ω
,所以f(x)=2sin(1 2
x+1 2
)-1-----------------(4分)π 3
则当
x+1 2
=2kπ-π 3
即x=4kπ-π 2
(k∈Z)时,f(x)的最小值-3------(5分)5π 3
当
x+1 2
=2kπ+π 3
即x=4kπ+π 2
(k∈Z)时,f(x)的最大值1-------(6分)π 3
(Ⅱ)由f(B)=1,得2sin(
B+1 2
)-1=1,解得B=π 3
-------------(8分)π 3
∴2R=
=b sinB
=6------------------------(10分)3 3 3 2
又由余弦定理知b2=a2+c2-2accosB=(a+c)2-3ac,∴ac=9
则sinAsinC=
•a 2R
=c 2R
-------------------------(12分)1 4

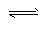 3R(g) △H>0,下图表示温度、压强的变化对上述反应的影响。下列表述正确的是
3R(g) △H>0,下图表示温度、压强的变化对上述反应的影响。下列表述正确的是