问题
探究题
已知:在一列数a1、a2、…、a2008中,任意相邻三个数的和都等于31,a3=m+n,a98=m﹣n+2,a2008=3m+n,m、n为实数,且2a1﹣3a3=11.
(1)请说明a98=a2,a2008=a1;
(2)求a的值.
答案
解:(1)∵任意相邻三个数的和都相等,
∴对于任意正整数k,都有ak+ak+1+ak+2=ak+1+ak+2+ak+3.
∴ak=ak+3.
∵98=3×32+2,2008=3×669+1,
∴a98=a2,a2008=a1,
(2)∵a98=m﹣n+2,a2008=3m+n,
∴a2=m﹣n+2,a1=3m+n.
∵a1+a2+a3=31,2a1﹣3a3=11,a3=m+n,
∴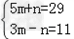 ,解得:
,解得: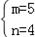 ,
,
故可得a2008=3m+n=19.
