问题
问答题
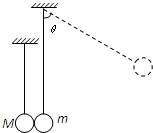
如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂.现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,下摆后在最低点与金属球发生弹性碰撞.在平衡位置附近存在垂直于纸面的磁场.已知由于磁场的阻尼作用,金属球将于再次碰撞前停在最低点处.求经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于45°.
答案
设小球m的摆线长度为l
小球m在下落过程中与M相碰之前满足机械能守恒:mgl(1-cosθ)=
mv02①1 2
m和M碰撞过程是弹性碰撞,故满足:
mv0=MVM+mv1 ②
mv02=1 2
mv12+1 2
MVM2 ③1 2
联立 ②③得:v1=
v0 ④m-M m+M
说明小球被反弹,且v1与v0成正比,而后小球又以反弹速度和小球M再次发生弹性碰撞,满足:
mv1=MVM1+mv2 ⑤
mv12=1 2
mv22+1 2
MVM12⑥1 2
解得:
v2=
|v1| ⑦m-M m+M
整理得:
v2=-(
)2v0⑧m-M m+M
故可以得到发生n次碰撞后的速度:
vn=|(
)nv0|⑨m-M m+M
而偏离方向为450的临界速度满足:
mgl(1-cos450)=
mv临界2⑩1 2
联立①⑨⑩代入数据解得,当n=2时,v2>v临界
当n=3时,v3<v临界
即发生3次碰撞后小球返回到最高点时与竖直方向的夹角将小于45°.
