问题
问答题
已知总体X的分布函数为
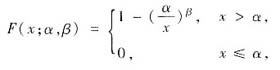
其中参数α＞0，β＞1，设X1，…，Xn是来自总体X的简单随机样本．
当β=2时，求未知参数α的最大似然估计量
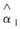与矩估计量
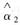，并讨论
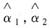是否为α的无偏估计．
答案
参考答案：β=2时，[*]
样本的似然函数为
[*]
当一切xi＞α即[*]时，L(α)是α的单调增函数，故α的最大似然估计[*]．
为计算[*]，需先求得X(1)的密度函数，即
[*]
故[*]
即[*]不是α的无偏估计．
令[*]，解得α的矩估计量[*]
由于[*]所以[*]为α的无偏估计．