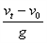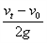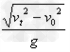问题
填空题
若f(n)=sin
|
答案
T=
=122π π 6
∴f(1)+f(2)+f(3)+…+f(12)
=
+1 2
+1+3 2
+3 2
+0-1 2
-1 2
-1-3 2
-3 2
-01 2
=0
从第一项起,每连续12项和为0
=8余6102 12
∴f(1)+f(2)+f(3)+…+f(102)
=8×0+f(97)+f(98)+…+f(102)
=f(1)+f(2)+…+f(6)
=
+1 2
+1+3 2
+3 2
+01 2
=2+3

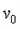 水平抛出,落地时速度大小为
水平抛出,落地时速度大小为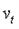 ,则它的运动时间为[ ]
,则它的运动时间为[ ]