设总体X服从正态分布N(μ，σ2)，从总体中抽取容量为36的简单随机样本，计算得样本均值
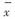=3.5，样本方差S2=4．(Ⅰ)若已知σ2=1，则μ置信度为0.95的置信区间为______；(Ⅱ)若σ2未知，则μ置信度为0.95的置信区间为______，单侧置信下限为______；(Ⅲ)若已知μ=1，则σ2置信度为0.95置信区间为______；(Ⅳ)若μ未知，则σ2置信度为0.95的置信区间为______；σ与lnσ2置信度为0.95的置信区间分别为______．
参考答案：17，3.83)，(2.83，4.18)，2.94，(6.70，17.10)，(2.63，6.81)，(0.97，1.92)
解析：
[分析]： 直接应用置信区间定义求解(也可以套用已知结果)．
(Ⅰ)已知X～N(μ，σ2)，μ的点估计为[*]．当σ2已知时，令[*]，即[*]，查表求得[*]，从而得μ置信度为1-α的置信区间[*]．
当n=36，1-α=0.95时，α=0.05，[*]，所求置信区间为[*]=(3.17，3.83)．
(Ⅱ)当σ2未知时，用样本方差S2估计，此时[*]，给定α查t分布上分位数表求得[*]，从而有
[*]
即
[*]
由此知μ置信度为1-α置信区间为
[*]
当n=36，1-α=0.95，[*]，查表得[*]=2.03，所求置信区间为
[*]
同理，选取tα(35)=t0.05(35)=1.69，使
[*]
由此得μ置信度为0.95的单侧置信下限为
[*]
(Ⅲ)由σ2估计量构造枢轴变量G从而求得σ2置信区间．已知μ=1，总体X～N(1，σ2)，因此根据等尾置信区间对给定X=0.05，由[*]查表求得上分位数[*]，于是有
[*]
即
[*]
其中[*]，又[*]，所以[*]，故[*]．将S2=4，[*]代入得[*]．于是σ2置信度为0.95置信区间[*]．
(Ⅳ)μ未知，考虑样本方差
[*]
令[*]
则[*]
即[*]
将S2=4，[*]代入得σ2置信度为0.95置信区间[*]．
因为当x＞0时，x2，lnx都是x的单调增函数，所以有
[*]
[*]
故σ与lnσ2置信度为0.95置信区间分别为[*]=(1.62，2.61)，与(ln2.63，ln6.81)=(0.97，1.92)．