问题
解答题
已知两点A（2，3）、B（4，1），直线l：x+2y－2=0，在直线l上求一点P.
（1）使|PA|+|PB|最小；
（2）使|PA|－|PB|最大.
答案
（1）P（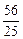
，－
） （2）P（8，－3）
（1）可判断A、B在直线l的同侧，设A点关于l的对称点A1的坐标为（x1，y1）.
由两点式求得直线A1B的方程为y=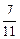
（x－4）+1，直线A1B与l的交点可求得为
P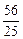（，－）.由平面几何知识可知|PA|+|PB|最小.
（2）由两点式求得直线AB的方程为y－1=－（x－4），即x+y－5=0.
直线AB与l的交点可求得为P（8，－3），它使|PA|－|PB|最大.