问题
填空题
设总体X的概率密度为
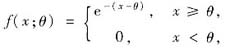
(X1，X，…，Xn)是来自总体X的简单随机样本，则未知参数θ的最大似然估计量
=______．
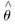答案
参考答案：min{X1，X2，…，Xn}
解析：
[分析]： 参数θ的似然函数为
[*]
由此可见，其似然方程无解，需要直接求其似然函数
[*]
的最大值．当x1，x2，…，xn＜θ时L(θ)=0，而当x1，x2，…，xn≥θ，即min{x1，x2，…，xn}≥θ时L(θ)随θ的增大而增大，可见当θ=min{x1，x2，…，xn}时L(θ)达到最大值．故θ的最大似然估计量为min{X1，X2，…，Xn