问题
单项选择题
设随机变量X在区间[-4,1]上服从均匀分布,Y~N(2,σ2),X和Y的概率密度分别记为f1(x)和f2(x).如果函数
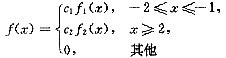
(其中C1>0,C2>0是常数)是某随机变量的概率密度,则C1,C2应满足
答案
参考答案:B
解析:
[分析]: X的概率密度为
[*]
可得
[*]
因为Y的概率密度曲线y=f2(x)关于直线x=2对称,所以
[*]
由概率密度的性质,有
[*]
即
2c1+5c2=10.
