问题
解答题
关于x的一元二次方程为（ｍ－1）x2－2ｍx＋ｍ＋1＝0
（1）求出方程的根；
（2）ｍ为何整数时，此方程的两个根都为正整数？
答案
（1）
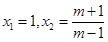；（2）m=2或m=3
题目分析：(1)、△=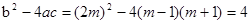
>0,所以此方程有两个不相等的实数根：
,
；
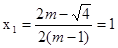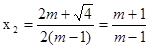（2）、当m为整数时，m-1与m+1为连续奇数或连续偶数，若方程的两个根都为正整数，则m+1能被m—1整除，这样的连续奇数为1、3，连续偶数为2、4，所以m=2或m=3.
试题解析：(1)、方程根的判别式△=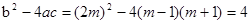>0,
所以此方程有两个不相等的实数根：,；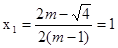
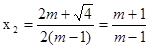（2）、∵m为整数，（m+1）-（m-1）=2
∴m-1与m+1为连续奇数或连续偶数
又∵方程的两个根都为正整数
∴m+1能被m—1整除
当m-1与m+1为连续奇数时，m-1=1，m+1=3，此时，m=2；
当m-1与m+1为连续偶数时，m-1=2，m+1=4，此时，m=3；
综上所述，m=2或m=3.