问题
解答题
（本小题满分12分）已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半，求：
(1) 动点M的轨迹方程；
(2) 若N为线段AM的中点，试求点N的轨迹．
答案
(1) x2＋y2＝16； (2) 以(1,0)为圆心，2为半径的圆．
题目分析：(1)设动点M(x，y)为轨迹上任意一点，则点M的轨迹就是集合P＝{M||MA|＝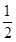
|MB|}．
由两点间距离公式，点M适合的条件可表示为
＝
.
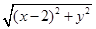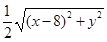平方后再整理，得x2＋y2＝16. 可以验证，这就是动点M的轨迹方程．
(2)设动点N的坐标为(x，y)，M的坐标是(x1，y1)．
由于A(2,0)，且N为线段AM的中点，
所以x＝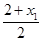
，y＝
.
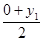所以有x1＝2x－2，y1＝2y.①
由(1)知，M是圆x2＋y2＝16上的点，
所以M的坐标(x1，y1)满足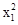
＋
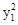＝16.②
将①代入②整理，得(x－1)2＋y2＝4. 所以N的轨迹是以(1,0)为圆心，2为半径的圆．
点评：求曲线的轨迹方程常采用的方法有直接法、定义法、相关点代入法、参数法。本题主要是利用直接法和相关点代入法，直接法是将动点满足的几何条件或者等量关系，直接坐标化，列出等式化简即得动点轨迹方程。相关点代入法 是根据相关点所满足的方程，通过转换而求动点的轨迹方程。