问题
解答题
(本小题满分12分)已知点P(6,4)与定直线l1:y=4x,直线l2过点P与直线l1相交于第一象限内的点Q,且与x轴的正半轴交于点M,求使△OMQ面积最小的直线l2的方程.
答案
l2的直线方程为x+y-10=0.
:设M(m,0),则直线l2的方程为
4x+(m-6)y-4m="0. " (*)
与y=4x联立方程组,得yQ=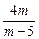 .
.
∵yQ>0,且m>0,
∴S△OMQ=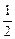 ·m·yQ=
·m·yQ=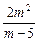 ,且m-5>0.
,且m-5>0.
令m-5=t,则t>0,
∴S△OMQ= =2(10+t+
=2(10+t+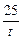 )
)
≥2(10+2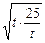 )=40.
)=40.
当且仅当t=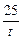 ,即t=5时,S△OMQ取最小值40.
,即t=5时,S△OMQ取最小值40.
此时,m=10.把m=10代入(*)式,得
l2的直线方程为x+y-10=0.

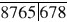 缺失,余留牙正常。可摘局部义齿设计为
缺失,余留牙正常。可摘局部义齿设计为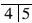 三臂卡环,舌杆大连接体。此义齿最容易出现的不稳定表现是()
三臂卡环,舌杆大连接体。此义齿最容易出现的不稳定表现是()