问题
解答题
解下列方程(每小题4分,共12分)
(1)x2-2x=0
(2)4x2-8x-1=0(用配方法)
(3)3x2-1=4x(公式法)
答案
(1)x1=0,x2=2 (2)x1=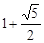 ,x2=
,x2=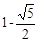 (3)x1=
(3)x1=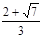 x2=
x2=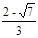
题目分析:(1)观察方程特点,没有常数项,适合用因式分解法解.(2)第一步把-1移到等式右边,第二步除以4,第三步两边加1,第四步开方.(3)用公式法时,首先把方程化成一般式,确定a、b、c的值,然后用判别式判断方程解的情况,最后再使用公式.
试题解析:(1)原方程化为:x(x-2)=0,x=0或x-2=0,所以x1=0,x2=2.
(2)原方程化为:x2-2x=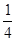 ,x2-2x+1=
,x2-2x+1=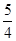 ,(x-1)2=
,(x-1)2=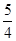 ,x-1=±
,x-1=±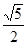 ,所以原方程的解为:x1=
,所以原方程的解为:x1=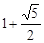 ,x2=
,x2=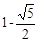 .
.
(3)原方程可化为:3x2-4x-1=0,a=3,b=-4,c=-1,△=(-4)2-4×3×(-1)=28>0,原方程有两个不相等的实数根,x1=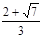 x2=
x2=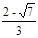 .
.
