问题
问答题
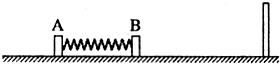
如图所示,质量分别为mA=6kg,mB=2kg的A、B两个小物块用细线栓接静止在光滑的水平面上,中间放一被压缩的轻弹簧,左端与A连接,右端与B不连接.现剪断细线,A、B被弹簧弹开,离开弹簧时,B物体的速度为6m/s,此后与右侧的挡板发生碰撞,碰撞没有能量损失.求:
①细线被剪断前,弹簧的弹性势能:
②B物体被挡板反弹后,通过弹簧再次与A发生作用的过程中,弹簧具有弹性势能的最大值.
答案
(1)设B离开弹簧时,A的瞬时速度为vAO,细线被剪断前,弹簧的弹性势能为△P1
由动量守恒定律:mAvA0=mBvB0
解得:vA0=4m/s
再根据能量守恒定律:△P1=
mA1 2
+vA 20
mB1 2
=48J.v 2B0
(2)当B第一次反弹,开始压缩弹簧,A、B具有相同速度V时弹性势能最大,
设为△P2由动量守恒定律:mAvA0+mBvB0=(mA+mB)v
再根据能量守恒定律:△P2=
mA1 2
+vA 20
mB1 2
-v 2B0
(mA+mB)1 2
=12Jv 2
答:①细线被剪断前,弹簧的弹性势能为48J.
②弹簧具有弹性势能的最大值为12J.
