问题
问答题
已知函数f(x)的定义域为R，且对任意的实数x，导函数f’(x)满足0＜f’(x)＜2且f’(x)≠1．常数c1为方程f(x)-x=0的实数根，常数c2为方程f(x)-2x=0的实数根．
若对任意的闭区间[a，b]
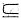R，总存在x0∈(a，b)，使等式f(b)-f(a)=(b-a)f’(x0)成立．
求证：方程f(x)-x=0不存在异于c1的实数根；
答案
参考答案：
假设存在实数c0，c1≠c0且f(c0)-c0=0．不妨设c0＜c1，则存在c3∈(c0，c1)，使等式f(c1)-f(c0)=(c1-c0)f’(c3)成立，即f’(c3)(c1-c0)=c1-c0，即f’(c3)=1，这与f’(x)≠1矛盾，所以假设不成立，故方程f(x)-x=0不存在异于c1的实数根．