某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
(1)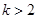
(2)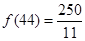
(3)当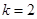 时完成订单任务的时间最短,此时生产A,B,C三种部件的人数分别为44,88,68
时完成订单任务的时间最短,此时生产A,B,C三种部件的人数分别为44,88,68
解:(Ⅰ)设完成A,B,C三种部件的生产任务需要的时间(单位:天)分别为 由题设有
由题设有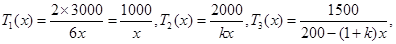
期中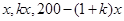 均为1到200之间的正整数.
均为1到200之间的正整数.
(Ⅱ)完成订单任务的时间为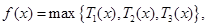 其定义域为
其定义域为
 易知,
易知, 为减函数,
为减函数,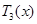 为增函数.注意到
为增函数.注意到
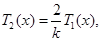 于是
于是
(1)当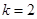 时,
时,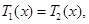 此时
此时
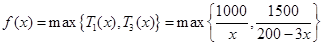 ,
,
由函数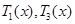 的单调性知,当
的单调性知,当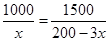 时
时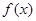 取得最小值,解得
取得最小值,解得
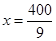 .由于
.由于
 .
.
故当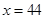 时完成订单任务的时间最短,且最短时间为
时完成订单任务的时间最短,且最短时间为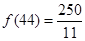 .
.
(2)当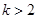 时,
时,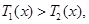 由于
由于 为正整数,故
为正整数,故 ,此时
,此时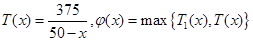 易知
易知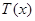 为增函数,则
为增函数,则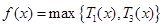
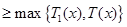
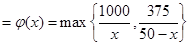 .
.
由函数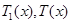 的单调性知,当
的单调性知,当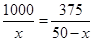 时
时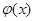 取得最小值,解得
取得最小值,解得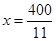 .由于
.由于
此时完成订单任务的最短时间大于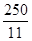 .
.
(3)当 时,
时, 由于
由于 为正整数,故
为正整数,故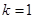 ,此时
,此时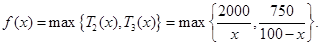 由函数
由函数 的单调性知,
的单调性知,
当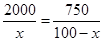 时
时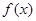 取得最小值,解得
取得最小值,解得 .类似(1)的讨论.此时
.类似(1)的讨论.此时
完成订单任务的最短时间为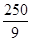 ,大于
,大于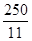 .
.
综上所述,当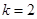 时完成订单任务的时间最短,此时生产A,B,C三种部件的人数
时完成订单任务的时间最短,此时生产A,B,C三种部件的人数
分别为44,88,68.
【点评】本题为函数的应用题,考查分段函数、函数单调性、最值等,考查运算能力及用数学知识分析解决实际应用问题的能力.第一问建立函数模型;第二问利用单调性与最值来解决,体现分类讨论思想
