问题
问答题
设二次型
xTAx=ax21+2x22-x23+8x1x2+2bx1x3+2cx2x3 矩阵A满足AB=0,其中

(Ⅰ)用正交变换化二次型xTAx为标准形,并写出所用正交变换.
(Ⅱ)判断矩阵A和B是否合同.
答案
参考答案:AB=0知λ=0是矩阵A的特征值且矩阵B的列向量(1,0,1)T是矩阵A属于特征值λ=0的特征向量.故有
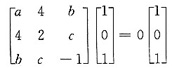
于是
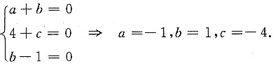
由矩阵A的特征多项式
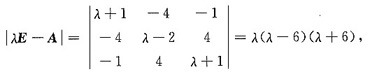
得矩阵A的特征值为:6,0,-6.
由(6E-A)x=0得矩阵A属于特征值6的特征向量为(1,2,-1)T
由(-6E-A)x=0得矩阵A属于特征值一6的特征向量为(-1,1,1)T
实对称矩阵特征值不同特征向量相互正交,单位化有
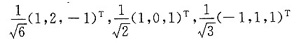
那么令

则有xTAx=yTAy=6y21-6y23.
(Ⅱ)不合同,因为xTAx=6y21-6y23,xTBx=(x1+x3)2=y21,它们的正负惯性指数不一样,所以不合同.
