问题
解答题
设等腰三角形的三条边分别为3、m、n，已知m、n是关于x的方程x2﹣4x+k=0的两个根，求k的值．
答案
4或3.
题目分析：分两种情况：①当m和n都是腰长时，方程有两个相等的实数根，根据△=0可得k的值；②当m，n一个是腰长，一个是底边长时，那么x=3是方程的一个根，把x=3代入x2-4x+k=0可得k的值．
试题解析：①当m和n都是腰长时，方程有两个相等的实数根，那么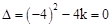
，解得k=4.
当k=4时，原方程为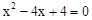
，解得：
.
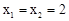2，2，3能够组成三角形，符合题意.
②当m,n一个是腰长，一个是底边长时，那么x=3是方程的一个根，
将x=3代入可得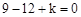
，解得k=3.
当k=3时，原方程为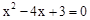
，解得：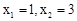
.
1，3，3能够组成三角形，符合题意.
∴k的值是4或3.