问题
问答题
设总体X的概率密度为
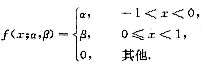 其中α和β是未知参数,利用总体X的如下样本值-0.5,0.3,-0.2,-0.6,-0.1,0.4,0.5,-0.8,求α的矩估计值和最大似然估计值.
其中α和β是未知参数,利用总体X的如下样本值-0.5,0.3,-0.2,-0.6,-0.1,0.4,0.5,-0.8,求α的矩估计值和最大似然估计值.
答案
参考答案:先求矩估计值[*].
[*],而[*]
[*]
令E(X)=[*],即[*].解得[*].
再求最大似然估计值[*].
在给定的8个样本值中,属(-1,0)的有5个,属[0,1)的有3个,故似然函数为
[*]
取对数,得 ln L(α)=5ln α+3ln(1-α),
两边对α求导,得[*]
令 [*],得[*](显然这时L(α)最大).
解析:
[分析]: 由f≥0和[*],得到α≥0,β≥0且α+β=1.不妨将f(x;α,β)改写成
[*]
显然,[*]
有了E(X)不难求出矩估计值.
最大似然估计值可由f(x;α)写出似然函数[*],再求得.
