问题
问答题
计算二重积分
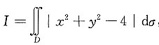 ,其中D是由y=|x|与y=2所围成的平面区域.
,其中D是由y=|x|与y=2所围成的平面区域.
答案
参考答案:[分析与求解] 由于积分区域D关于y轴对称,被积函数f(x,y)=|x2+y2-4|是变量x的偶函数,从而
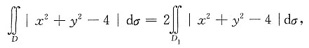
其中D1=D∩{x≥0}={(x,y)|0≤x≤2,x≤y≤2}.又因被积函数关于变量x,y对称,即满足f(x,y)=f(y,x),故
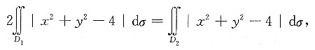
其中D2是正方形区域{(x,y)|0≤x≤2,0≤y≤2}.
为了去掉被积函数中的绝对值符号,将积分区域D2用圆弧x2+y2=4分成两个部分区域,可得
D21={(x,y)|0≤x≤2,0≤y≤2,x2+y2≤4},
D22={(x,y)|0≤x≤2,0≤y≤2,x2+y2≥4}.
于是
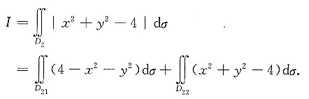
设x=rcosθ,y=rsinθ,在极坐标系(r,θ)中
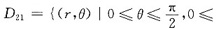
 从而
从而
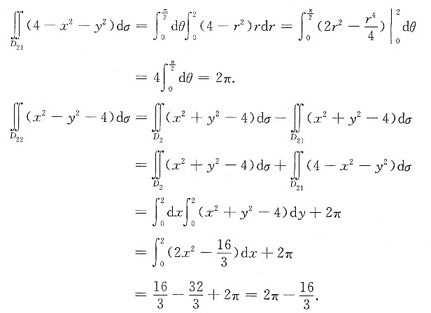
有关的积分区域如图: