问题
问答题
已知随机变量X1，X2，X3，X4相互独立，X1与X2都在区间(0，1)上服从均匀分布，X3与X4都服从参数为
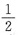的0-1分布，记Y=X1+X2+X3X4，求Y的分布函数FY(y)及概率密度fY(y)．
答案
参考答案：[解答] 由题设知X1与X2的概率密度为
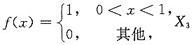
与X4概率分布
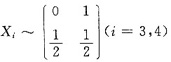，记Y1=X1+X2，Y2=X3X4，因为Xi相互独立，所以Y1与Y2独立，且Y2的概率分布为
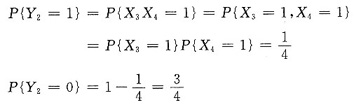
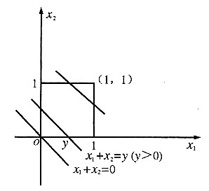
由于X1与X2的联合密度为
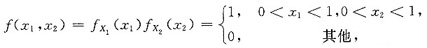
因此Y1=X1+X2的分布函数
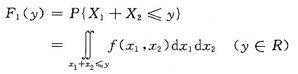
当y≤0时，F1(y)=0；
当0＜y≤1时，
；
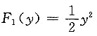当1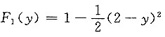
，
当2＜y时，F1(y)=1．
综上得，
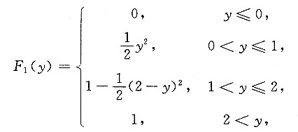
因此Y1=X1+X2的概率密度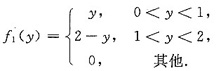
由于Y=Y1+Y2，Y1与Y2独立，Y2为离散型随机变量，因而应用全概公式可求得y的分布函数FY(y)，进而求得概率密度是fY(y)．
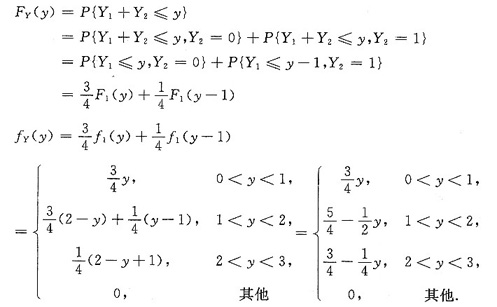
[说明] ①我们可以用卷积公式求得Y1=X1+X2的概率密度f1(y)．事实上
故当y≤0或y≥2时f1(y)=0；当0＜y＜1时，；当1≤y＜2时，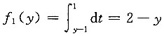
；
②如果将题目中的X1与X2改为：都服从标准正态分布N(0，1)，那么Y＝X1+X2+X3X4的分布函数FY(y)与概率密度FY(y)各为多少
由题设知Y1=X1+X2～N(0，2)，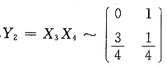
Y1与Y2相互独立，故Y=Y1+Y2的分布函数
FY(y)=P{Y1+Y2≤y}=P{Y1+Y2≤y，Y2=0)+P{Y1+Y2≤y，Y1=1}
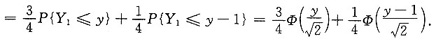
概率密度
