问题
选择题
已知直线l1：(k－3)x＋(4－k)y＋1＝0，与l2：2(k－3)x－2y＋3＝0平行，则k的值是( )
A．1或3
B．1或5
C．3或5
D．1或2
答案
答案：C
当k-3=0时，求出两直线的方程，检验是否平行；当k-3≠0时，由一次项系数之比相等且不等于常数项之比，求出k的值．
解：由两直线平行得，当k-3=0时，两直线的方程分别为 y=-1 和 y=3/2，显然两直线平行．当k-3≠0时，由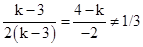
，可得 k=5．综上，k的值是 3或5，
故选 C．