问题
问答题
设随机变量X的密度函数为f(x)，已知方差D(X)=1，而随机变量Y的密度函数为f(-y)，且X与Y的相关系数为-
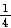，记Z=X+Y．
(Ⅰ)求E(Z)，D(Z)的值；
(Ⅱ)用切比雪夫不等式估计P(|Z|≥2)．
答案
参考答案：(Ⅰ)[*]
令y=-x，则[*]
所以 E(Z)=0．
已知D(X)=1，D(Y)=E(Y2)-[E(Y)]2=E(Y2)-[-E(X)]2，
而[*]
所以D(Y)=E(Y2)-[-E(X)]2=E(X2)-[E(X)]2=D(X)=1．
D(Z)=D(X+Y)=D(X)+D(Y)+2cov(X，Y)
[*]
[*]，即D(Z)=1.5．
(Ⅱ)[*]
解析：
[分析]： 函数f(x)与f(-x)的图形关于y轴对称，故X与Y的数学期望也应关于y轴对称，即E(X)=-E(Y)．f(x)与f(-x)反映随机变量离散程度的方差是一致的，即D(X)=D(Y)．
切比雪夫不等式为 [*]