问题
解答题
关于x的一元二次方程x2+3x+m﹣1=0的两个实数根分别为x1，x2．
（1）求m的取值范围；
（2）若2（x1+x2）+x1x2+10=0，求m的值．
答案
（1）m≤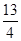
；（2）-3.
题目分析：（1）因为方程有两个实数根，所以根的判别式要大于等于0，即△≥0，据此即可求出m的取值范围；（2）根据一元二次方程根与系数的关系，将x1+x2=-3，x1x2=m-1代入2（x1+x2）+x1x2+10=0，解关于m的方程即可．
试题解析：（1）∵方程有两个实数根，
∴△≥0，
∴9-4×1×（m-1）≥0，
解得m≤；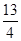
（2）∵x1+x2=-3，x1x2=m-1，
又∵2（x1+x2）+x1x2+10=0，
∴2×（-3）+m-1+10=0，
∴m=-3．