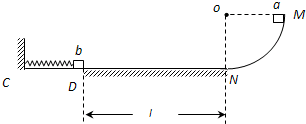
如图，半径为R，光滑的14圆弧轨道固定在竖直平面内，与水平轨道C

问题问答题

如图，半径为R，光滑的

圆弧轨道固定在竖直平面内，与水平轨道CN相接．水平轨道的CD段光滑、DN段粗糙．一根轻质弹簧一端固定在C处的竖直面上，另一端与质量为2m的小物块b刚好在D点接触但不连接，弹簧处于自然长度．质量为m的小物块a从圆弧轨道顶端M点由静止释放并下滑，后与物块b碰撞后一起向左压缩弹簧（两物块不粘连）．若

=l，物块a、b与轨道DN的动摩擦因数分别为μ₁=0.1和μ₂=0.2，重力加速度为g．求：

（1）小物块a第一次经过N点时，轨道对a支持力的大小．

（2）小物块a与物块b碰撞后瞬间的共同速度大小．

（3）若a、b能且只能发生一次碰撞，试讨论l与R的关系．

答案

（1）物块a由M到N过程中，由机械能守恒有：mgr=

①

由牛顿第二定律有：F-mg=

②

联立①②解得：轨道对a支持力 F=3mg

（2）物块a从N滑至D过程中，由动能定理有：-μ1mgl=

2D1

③

物块a、b在D点碰撞，根据动量守恒有：mv_D1=3mv_D2④

解得两物块在D点向左运动的速度 vD2=

2g(R-0.1l)

（3）a、b一起压缩弹簧后又返回D点时速度大小v_D3=

2g(R-0.1l)

⑤

由于物块b的加速度大于物块a的加速度，所以经过D点后，a、b两物块分离，同时也与弹簧分离．讨论：①假设a在D点时的速度v_D1=0，即l=10R，要使a、b能够发生碰撞，则l＜10R ②假设物块a滑上圆弧轨道又返回，最终停在水平轨道P点，物块b在水平轨道上匀减速滑至P点也恰好停止，设

=x，则

=l-x，

根据能量守恒，对a物块 μ₁mg（l+x）=

2D3

⑥

对b物块μ₂2mg（l-x）=

2mv

2D3

⑦

由以上两式解得：x=

l，⑧

将x=

l代人 μ₁mg（l+x）=

2D3

解得：l=

R ⑨

要使a、b只发生一次碰撞，则l≥

R ⑩

综上所述，当10R＞l≥

R时，a、b能且只能发生一次碰撞．

答：

（1）小物块a第一次经过N点时，轨道对a支持力的大小为3mg．

（2）小物块a与物块b碰撞后瞬间的共同速度大小为

2g(R-0.1l)

．

（3）若a、b能且只能发生一次碰撞，讨论l与R的关系见上．