问题
问答题
设f(x)在[0，1]上连续，在(0，1)内可导，且f(0)=f(1)，常数a＞0与b＞0．求证：存在满足0＜ξ＜η＜1的ξ与η使得af′(ξ)+bf′(η)=0．
答案
参考答案：
[分析]： 本题属中值定理的证明题中要证存在两个不同点ξ和η，这种问题应将[0，1]分为两个区间[0，c]和[c，1]，然后在这两个区间上分别用拉格朗日中值定理．问题的关键在于c点的选取，为此，利用拉格朗日中值定理得
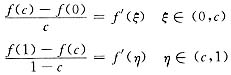
从而有
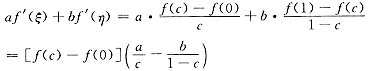
若能选得c∈(0，1)，使
，则必有af′(ξ)+bf′(η)=0，问题得以证明.显然
．
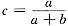[证] 令
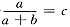，在[0，c]和[c，1]上分别对f(x)用拉格朗日定理得
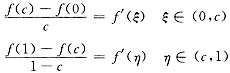
此时，
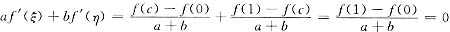
[评注] 题给出了此类问题求解的一种常用方法．