问题
填空题
已知：二次函数y=ax2+bx+c（a≠0）的图象如右图所示，下列结论中：①abc＞0；②2a-b＜0；③a+b＜m（am+b）（m≠1的实数）；④（a+c）2＜b2；⑤a＞1．其中正确的是（）（只需填序号）．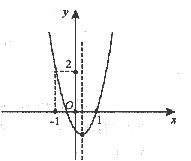
答案
参考答案：①⑤
解析：
本题考查二次函数的对称轴、开口方向、系数的符号、及函数中的数形结合思想．从开口方向向上可知a＞0，与y轴交点在x轴下方，则c＜0，又因为对称轴[*]，∴b＜0，abc＞0，①对；[*]，∴-b＜2a，∴2a+b＞0，②不对；x=1，y1=a+b+c；x=m，y2=am2+mb+c=m(am+b)+c，当m＞1，．y2＞y1；当m＜1，y2＜y1，所以不能确定，③不对；
∵(a+c+b)(a+c-b)=(a+b+c)(a-b+c)，
当x=1时，y=a+b+c=0；x=-1时，y=a-b+c＞0，
∴(a+b+c)(a-b+c)=0，
∴(a+c)2-b2=0，
所以④不对；
x=-1，a-b+c=2；x=1，a+b+c=0，
∴2a+2c=2，a+c=1，a=1-c=1+(-c)＞1，所以⑤当选．