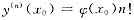问题
填空题
设y=(x-1)(x-2)2(x-3)3(x-4)4，则y′″(3)=______．
答案
参考答案：L
解析： 令
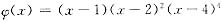
则
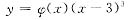
设
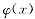在x=3处的幂级数展开式为
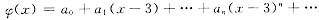
则
y-(x-3)3[a0+a1(x-3)+…+an(x-3)n+…]
=a0(x-3)3+a1(x-3)4+…+an(x-3)n+3+…
从而
y′″t(3)=a0·3!=6a0
显然
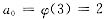，故y′″(3)=12．
[评注] 由本题的分析可得到一个常用的结论：若
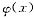在x0的某邻域内可展开为幂级数，
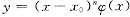(n为正整数)，则
y(k)(x0)=0 k=1，2，…，n-1
