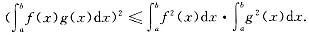问题
问答题
设f(x)在[0,+∞)上连续,且
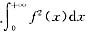 收敛,令
收敛,令
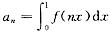 ,证明:
,证明:
 收敛.
收敛.
答案
参考答案:[证明] 令nx=t,则
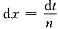
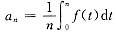
从而
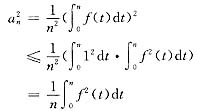
又由于
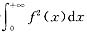 收敛,设
收敛,设
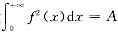 ,则
,则
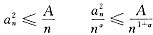
当a>0时,级数
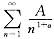 收敛,故级数
收敛,故级数
 收敛.
收敛.
[评注] 本题在证明过程中用到一个重要的积分不等式,即Cauchy积分不等式
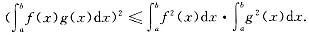
设f(x)在[0,+∞)上连续,且
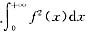 收敛,令
收敛,令
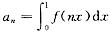 ,证明:
,证明:
 收敛.
收敛.
参考答案:[证明] 令nx=t,则
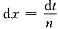
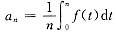
从而
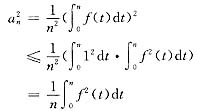
又由于
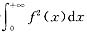 收敛,设
收敛,设
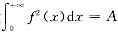 ,则
,则
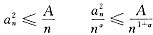
当a>0时,级数
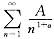 收敛,故级数
收敛,故级数
 收敛.
收敛.
[评注] 本题在证明过程中用到一个重要的积分不等式,即Cauchy积分不等式