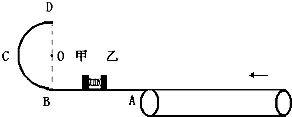
如图所示,光滑的水平面AB(足够长)与半径为R=0.8m的光滑竖直半圆轨道BCD在B点相切,D点为半圆轨道最高点.A点的右侧等高地放置着一个长为L=20m、逆时针转动速度为v0=10m/s的传送带.用轻质细线连接甲、乙两物体,中间夹一轻质弹簧,弹簧与甲乙两物体不栓接.甲的质量为m1=3kg,乙的质量为m2=1kg,甲、乙均静止在光滑的水平面上.现固定乙球,烧断细线,甲离开弹簧后进入半圆轨道并可以通过D点,且过D点时对轨道的压力恰好等于甲的重力.传送带与乙物体间摩擦因数为0.6,重力加速度g取l0m/s2,甲、乙两物体可看作质点.
(1)求甲球离开弹簧时的速度.
(2)若甲固定,乙不固定,细线烧断后乙可以离开弹簧后滑上传送带,求乙在传送带上滑行的最远距离.
(3)甲乙均不固定,烧断细线以后,求甲和乙能否再次在AB面上水平碰撞?若碰撞,求再次碰撞时甲乙的速度;若不会碰撞,说明原因.
(1)甲离开弹簧以后,机械能守恒:
m11 2
=m1g•2R+v 20
m11 2 v 2D
过D点时对轨道的压力恰好等于甲的重力,根据牛顿第二定律得:
2m1g=m1v 2D R
解得:v0=4
m/s3
(2)根据能量守恒得:
Ep=
m11 2
=v 20
m21 2 v 2乙
得:v乙=12m/s
之后乙滑上传送带匀减速运动,根据牛顿第二定律得:
μmg=ma
得:a=6m/s2
速度为零时离A端最远,最远距离为:
x=
=12m<20mv 2乙 2a
即乙在传送带上滑行的最远距离为12m.
(3)甲乙分离分离过程中,动量守恒,选v1的方向为正,根据动量守恒得:
m1v1=m2v2
甲乙弹簧系统能量守恒:
Ep=
m11 2
=v 20
m11 2
+v 21
m21 2 v 22
解得:
=2v 1
m/s,v2=63
m/s3
之后甲沿轨道上滑,设上滑最高点高度为h,
则
m11 2
=m1ghv 21
得h=0.6m<0.8m
则甲上滑不到等圆心位置就会返回,返回AB面上速度仍然是v1=2
m/s3
乙滑上传送带,因v2=6
m/s<12m/s,3
则乙先向右做匀减速运动,后向左匀加速.
由对称性可知返回AB面上速度仍然为v2=6
m/s3
所以甲和乙能再次在AB面上水平碰撞,再次碰撞时甲乙的速度大小分别是v1=2
m/s,v2=63
m/s3
答:(1)甲球离开弹簧时的速度大小是4
m/s.3
(2)若甲固定,乙不固定,细线烧断后乙可以离开弹簧后滑上传送带,乙在传送带上滑行的最远距离是12m.
(3)甲乙均不固定,烧断细线以后,甲和乙能再次在AB面上水平碰撞,再次碰撞时甲乙的速度大小分别是v1=2
m/s,v2=63
m/s3
