问题
选择题
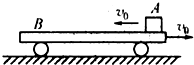
如图所示,足够长的 * * 板车B的质量为M,以水平速度υ0向右在光滑水平面上运动,与此同时,质量为m的小物体A从车的右端以水平速度υ0沿车的粗糙上表面向左运动.若物体与车面之间的动摩擦因数为μ,则在足够长的时间内( )
A.若M>m,物体A对地向左的最大位移是2M υ 20 μ(M+m)g
B.若M<m,小车B对地向右的最大位移是M υ 20 μmg
C.无论M与m的大小关系如何,摩擦力对平板车的冲量均为mυ0
D.无论M与m的大小关系如何,摩擦力的作用时间均为2Mυ0 μ(M+m)g
答案
规定向右为正方向,根据动量守恒定律有:Mv0-mv0=(M+m)v
解得:v=
.(M-m)v0 M+m
AB、A所受的摩擦力f=μmg,所以A的加速度a=μg,
根据v2-v02=2ax,若M>m,则共同的速度方向水平向右,则A相对于地面的最大位移大小x=
=v2-v02 2a
.v02 2μg
对B:加速度a′=
.μmg M
根据v2-v02=2a′x′
解得B相对于地面的最大位移大小:x′=
=v2-v02 -2 μmg M
.故A、B错误.2M2v02 μg(M+m)2
C、根据动量定理知,摩擦力对平板车的冲量等于平板车动量的变化量,即I=Mv-Mv0=
.故C错误.-2mMv0 m+M
D、根据动量定理得,-ft=Mv-Mv0,f=μmg,解得:t=
.故D正确.2Mυ0 μ(M+m)g
故选D.
