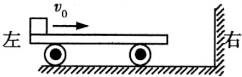
如图所示,一质量为m的平板车左端放有质量为M的滑块,滑块与平板车之间的动摩擦因数为μ开始时,平板车和滑块共同以速度v0沿光滑水平面向右运动,并与竖直墙壁发生碰撞,设碰撞时间极短,且碰撞后平板车速度大小保持不变,但方向与原来相反.平板车足够长,滑块不会滑出平板车右端,重力加速度为g.求:
(1)平板车第一次与墙壁碰撞后再次与滑块速度相同时,两者的共同速度;
(2)平板车第一次与墙壁碰撞后再次与滑块速度相同时,平板车右端距墙壁的距离.
(1)平板车与墙发生碰撞后以原速率弹回,此后平板车与木块所受的合外力为零,总动量守恒,取水平向右为正方向,则有
Mv0-mv0=(m+M)v
解得v=
v0,M-m M+m
当M>m,则v>0,方向向右.
当M<m,则v<0,方向向左.
(2)当M>m时,平板车与墙壁碰撞后先向左减速运动,后向右加速运动到与滑块速度相等,
设平板车向左运动的最大距离是x1,从最大距离处向右运动到速度与滑块速度相同时的距离为x2,
由动能定理得:-μMgx1=0-1 2 mv 20
μMgx2=1 2 mv 2
平板车右端距离墙壁的距离为△x=x1-x2=2m2v 20 μ(M+m)2g
当M<m,平板车一直减速到与滑块速度相等,
由动能定理得:-μMgx=1 2
-mv 2 1 2 mv 20
解得x=2m2v 20 μ(M+m)2g
两种情况下,平板车第一次与墙壁碰撞后再次与滑块速度相同时,平板车右端距墙壁的距离相等,即x=△x=
.2m2v 20 μ(M+m)2g
答:(1)平板车第一次与墙壁碰撞后再次与滑块速度相同时,两者的共同速度大小是
v0.M-m M+m
当M>m,则v>0,方向向右.当M<m,则v<0,方向向左.
(2)平板车第一次与墙壁碰撞后再次与滑块速度相同时,平板车右端距墙壁的距离是
.2m2v 20 μ(M+m)2g
