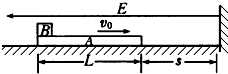
质量mA=3.0kg、长度L=0.60m、电量q=+4.0×10-5C的导体板A在绝缘水平面上,质量mB=1.0kg可视为质点的绝缘物块B在导体板A上的左端,开始时A、B保持相对静止一起向右滑动,当它们的速度减小到v0=3.0m/s时,立即施加一个方向水平向左、场强大小E=1.0×105N/C的匀强电场,此时A的右端到竖直绝缘挡板的距离为s,此后A、B始终处在匀强电场中,如图所示.假定A与挡板碰撞时间极短且无机械能损失,A与B之间(动摩擦因数μ1=0.25)及A与地面之间(动摩擦因数μ2=0.10)的最大静摩擦力均可认为等于其滑动摩擦力,g取10m/s2.试通过计算分析:(1)A在未与挡板相碰前A、B之间是否有相对滑动?(2)要使B恰好不从A上滑下,s应等于多少.
(1)A、B恰好不相对滑动时,两者之间的静摩擦力达到最大,则AB的最大加速度为
a0=
=2.5m/s2μ1mBg mB
若A、B一起作匀减速运动,则其加速度为
a=
=2m/s2<a0Eq+μ2(mA+mB)g mA+mB
所以A、B要一起作匀减速运动.
(2)设碰挡板前瞬间的速度为v,则有
v2-v02=-2as,
得v2=v02-2as
因与挡板相碰的过程无机械能损失,A碰撞挡板后只是速度反向,大小不变,
以后A、B组成的系统合外力为零,动量守恒,有
mAv-mBv=(mA+mB)v'
要使B恰好不从A上滑下,必然有
μ1mBgL=
mAv2+1 2
mBv2-1 2
(mA+mB)v′21 2
解得:s=2m
答:
(1)A在未与挡板相碰前A、B之间是没有发生相对滑动.
(2)要使B恰好不从A上滑下,s应等于2m.