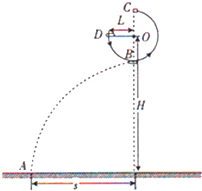
如图所示,在离地面H=5.45m的O处用长L=0.45m的不可伸长的细线挂一质量为90g的爆竹(火药质量忽略不计),把爆竹拉起至D点使细线水平伸直,点燃导火线后将爆竹无初速度释放,爆竹刚好到达最低点B时炸成质量相等的两块,一块朝相反方向水平抛出,落到地面上的A处,抛出的水平距离s=5m.另一块仍系在细线上继续做圆周运动通过最高点C.假设火药爆炸释放的能量全部转化为爆竹碎片的动能,空气阻力忽略不计,取g=10m/s2,求:
(1)爆炸瞬间反向抛出的那一块的水平速度v1的大小;
(2)继续做圆周运动的那一块通过最高点时的细线的拉力T的大小.
(3)火药爆炸释放的能量E.
(1)设爆竹的总质量为2m,刚好到达B时的速度为v,爆炸后抛出的那一块的水平速度为v1,做圆周运动的那一块的水平速度为v2,则对做平抛运动的那一块有:
H-L=
gt2,s=v1t,带入数据,得:v1=5m/s1 2
(2)爆竹从D点运动到B点的过程中机械能守恒,所以有2mgL=
×2mv2,1 2
爆竹爆炸前后动量守恒,所以有2mv=mv2-mv1,解得:v2=11m/s
设做圆周运动的那块通过最高点时的速度为vc,由机械能守恒定律可得:
mv22=1 2
mvc2+2mgL;1 2
设最高点时线对爆竹的拉力为T,则由牛顿第二定律可得:T+mg=mvc2 L
联立以上各式,解得:T=9.85N
(3)火药爆炸释放的能量为:E=
mv12+1 2
mv22-2mgL=2.88J1 2
答:(1)爆炸瞬间反向抛出的那一块的水平速度v1的大小为5m/s;
(2)继续做圆周运动的那一块通过最高点时的细线的拉力T的大小9.85N.
(3)火药爆炸释放的能量E为2.88J.
