（1）x+2y-1=0；（2) P。

(1)先由两直线方程联立解方程组求出交点坐标，然后根据所求直线与直线x+2y-3=0平行，求出斜率，从而写出点斜式方程再化成一般式即可.

(2)先求出MN的垂直平分线方程，它与直线x-y+4=0联立，解方程组可求出点P的坐标.

联立x-y=1与2x+y=2得解得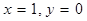

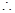直线x-y=1与2x+y=2的交点是 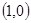                         ……2分

将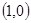代入x+2y+m=0求得m=-1                             ……3分

所求直线方程为x+2y-1=0                  

（法二）易知所求直线的斜率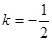，由点斜式得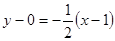

化简得x+2y-1=0                                       ……5分

2)解：方法一：由直线x－y＋4＝0，得y＝x＋4，点P在该直线上．

∴可设P点的坐标为(a，a＋4)．                                      ……2分

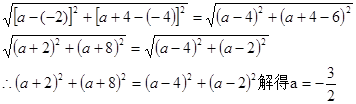∴               ……4

解得a＝－，从而a＋4＝－＋4＝. ∴P               ……5分