问题
填空题
圆x2＋y2－ax＋2＝0与直线l相切于点A(3,1)，则直线l的方程为________．
答案
x＋y－4＝0
由已知条件可得32＋12－3a＋2＝0，解得a＝4，此时圆x2＋y2－4x＋2＝0的圆心为C(2,0)，半径为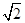
，则直线l的方程为y－1＝－
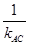(x－3)＝－x＋3，即x＋y－4＝0.
搜题请搜索小程序“爱下问搜题”
圆x2＋y2－ax＋2＝0与直线l相切于点A(3,1)，则直线l的方程为________．
x＋y－4＝0
由已知条件可得32＋12－3a＋2＝0，解得a＝4，此时圆x2＋y2－4x＋2＝0的圆心为C(2,0)，半径为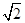，则直线l的方程为y－1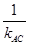＝－ (x－3)＝－x＋3，即x＋y－4＝0.