问题
问答题
设3阶对称矩阵A的特征值λ1=1，λ2=2，λ3=-2，又α1=(1，-1，1)T是A的属于λ1的一个特征向量．记B=A5-4A3+E，其中E为3阶单位矩阵．
(1) 验证α1是矩阵B的特征向量，并求B的全部特征值与特征向量；
(2) 求矩阵B．
答案
参考答案：(1) 容易验证Anα1=
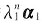(n=1，2，…)，于是
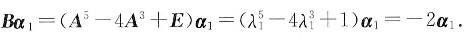
于是-2是矩阵B的特征值，k1α1是B属于特征值-2的全部特征向量(k1∈R，非零)．同理可求得矩阵B的另外两个特征值1和1．
因A为实对称矩阵，则B也为实对称矩阵，于是矩阵B属于不同特征值的特征向量是正交的．设B的属于1的特征向量为(x1，x2，x3)T，则有方程
x1-x2+x3=0．
于是求得B的属于1的全部特征向量为β=k2α2+k3α3，其中α2=(-1，0，1)Tα3=(1，1，0)T，k2，k3∈R，不全为零．
(2) 令矩阵P=(α1，α2，α3)=
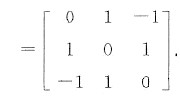
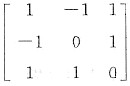．则P-1BP=diag(-2，1，1)，于是
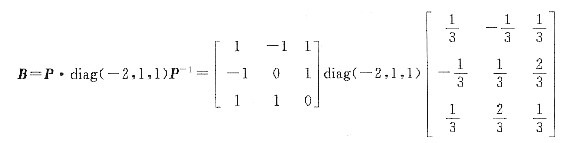
解析：[考点提示] 矩阵的特征向量与特征值．