问题
填空题
对于任意x∈[1,2]，都有(ax＋1)2≤4成立，则实数a的取值范围为________．
答案
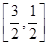
由不等式(ax＋1)2≤4在x∈[1,2]恒成立，得－2≤ax＋1≤2在x∈[1,2]恒成立，利用分类参数的方法得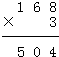
利用反比例函数的单调性得－
≤a≤
.
搜题请搜索小程序“爱下问搜题”
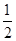对于任意x∈[1,2]，都有(ax＋1)2≤4成立，则实数a的取值范围为________．
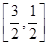
由不等式(ax＋1)2≤4在x∈[1,2]恒成立，得－2≤ax＋1≤2在x∈[1,2]恒成立，利用分类参数的方法得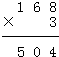利用反比例函数的单调性得－≤a≤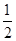.