问题
问答题
求抛物线y2=2x与直线y=x-4所围图形的面积．
答案
参考答案：
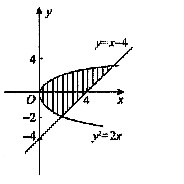
如右图所示，取y为积分变量，
联立方程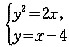
得交点纵坐标为y1=-2，y2=4，故所求面积为：
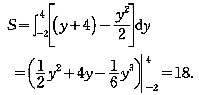
解析：
求平面图形的面积关键是画出平面图形并确定积分变量和积分限．
搜题请搜索小程序“爱下问搜题”
求抛物线y2=2x与直线y=x-4所围图形的面积．
参考答案：
如右图所示，取y为积分变量，
联立方程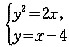得交点纵坐标为y1=-2，y2=4，故所求面积为：
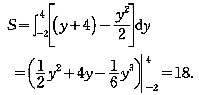
解析：
求平面图形的面积关键是画出平面图形并确定积分变量和积分限．