问题
问答题
已知函数f(x)=x3+ax+b的图像是曲线C,直线y=kx+1与曲线C相切于点(1,3).
(1)求函数f(x)的解析式;
(2)求函数f(x)的递增区间;
(3)求函数F(x)=f(x)-2x-3在区间上[0,2]的最大值和最小值.
答案
参考答案:
(1)∵切点为(1,3),∴k+1=3,得k=2.
∵f′(x)=3x2+a,∴f′(1)=3+a=2,得a=-1.则f(x)=x3-x+b.
由f(1)=3得b=3.∴f(x)=x3-x+3.
(2)由f(x)=x3-x+3得f′(x)=3x2-1,
令f′(x)=3x2-1>0,解得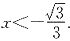 或
或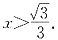
∴函数f(x)的增区间为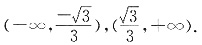
(3)F(x)=x3-3x,F′(x)=3x2-3,令F′(x)=3x2-3=0,得x1=-1,x2=1.
列出x,F′(x),F(x)关系如下:

∴当x∈[0,2]时,F(x)的最大值为2,最小值为-2.
